AI笔记(2):神经网络基础
1.算法基础与逻辑回归
逻辑回归(Logistic regression) 是一个用于二分类的算法。
1.1 二分类问题与机器学习基础
二分类就是输出 只有 {0,1} 两个离散值(也有 {-1,1} 的情况)。我们以一个「图像识别」问题为例,判断图片是否是猫。识别是否是「猫」,这是一个典型的二分类问题——0代表「非猫(not cat)」,1代表「猫(cat)」。

从机器学习的角度看,我们的输入 此时是一张图片,彩色图片包含RGB三个通道,图片尺寸为
。

有些神经网络的输入是一维的,我们可以将图片 (维度
)展平为一维特征向量(feature vector),得到的特征向量维度为
。我们一般用列向量表示样本,把维度记为
。
如果训练样本有 张图片,那么我们用矩阵存储数据,此时数据维度变为
。

- 矩阵
的行
代表了每个样本
特征个数
- 矩阵
的列
代表了样本个数。
我们可以对训练样本的标签 也做一个规整化,调整为1维的形态,标签
的维度为
。
1.2 逻辑回归算法
逻辑回归是最常见的二分类算法,它包含以下参数:
- 输入的特征向量:
,其中
是特征数量
- 用于训练的标签:
- 权重:
- 偏置:
- 输出:
输出计算用到了Sigmoid函数,它是一种非线性的S型函数,输出被限定在 之间,通常被用在神经网络中当作激活函数(Activation Function)使用。
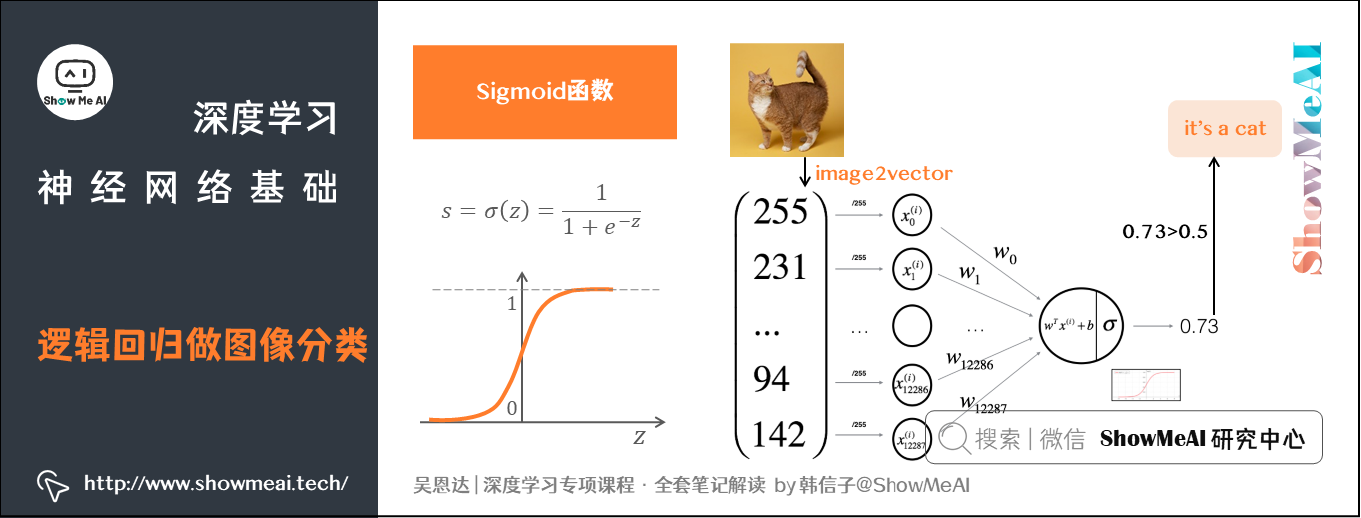
Sigmoid函数的表达式如下:
实际上,逻辑回归可以看作非常小的一个神经网络。
1.3 逻辑回归的损失函数

在机器学习中,**损失函数(loss function)**用于量化衡量预测结果与真实值之间的差距,我们会通过优化损失函数来不断调整模型权重,使其最好地拟合样本数据。
在回归类问题中,我们会使用均方差损失(MSE):
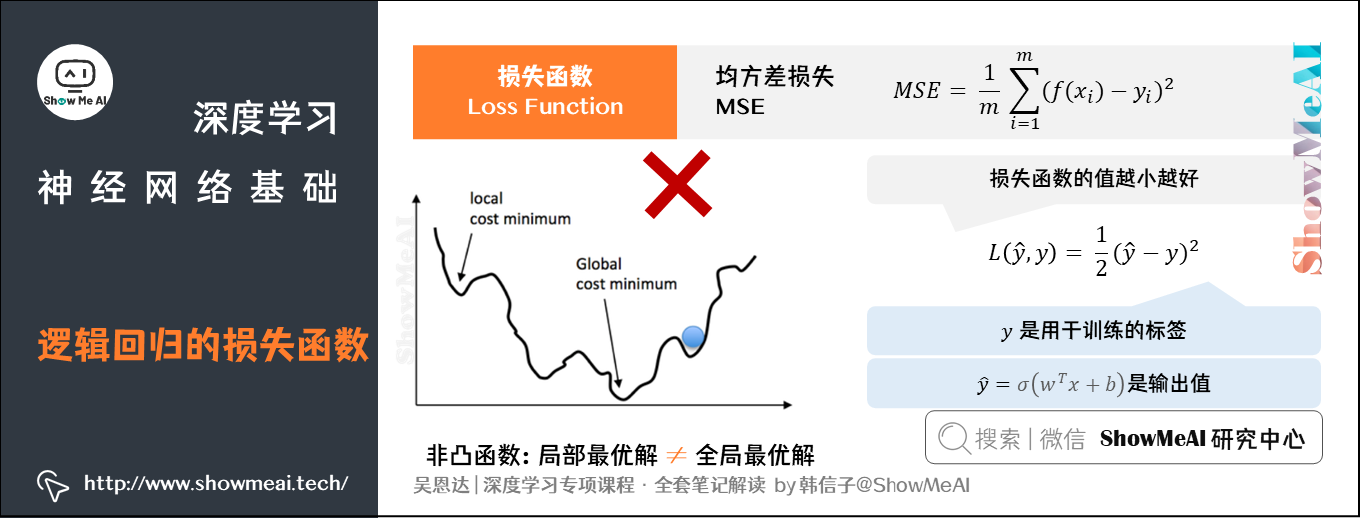
但是在逻辑回归中,我们并不倾向于使用这样的损失函数。逻辑回归使用平方差损失会得到非凸的损失函数,它会有很多个局部最优解。梯度下降法可能找不到全局最优值,从而给优化带来困难。
因此我们调整成使用对数损失(二元交叉熵损失):
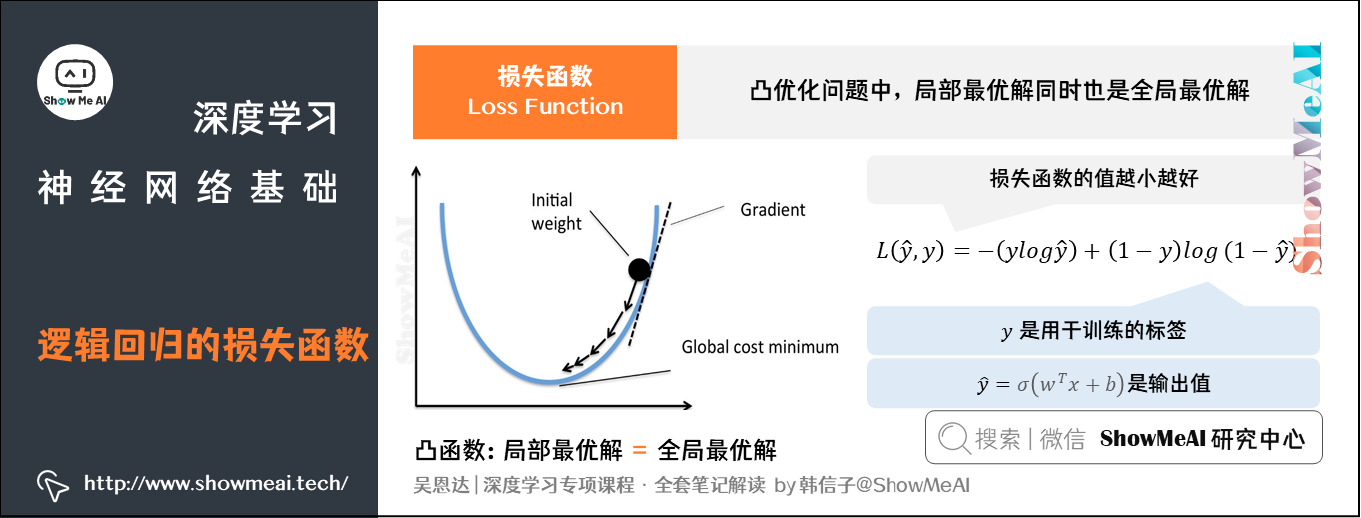
刚才我们给到的是单个训练样本中定义的损失函数,它衡量了在单个训练样本上的表现。我们定义代价函数(Cost Function,或者称作成本函数)为全体训练样本上的表现,即 个样本的损失函数的平均值,反映了
个样本的预测输出与真实样本输出
的平均接近程度。
成本函数的计算公式如下:
2.梯度下降法(Gradient Descent)

刚才我们了解了损失函数(Loss Function)与成本函数定义,下一步我们就要找到最优的 和
值,最小化
个训练样本的Cost Function。这里用到的方法就叫做梯度下降(Gradient Descent)算法。
在数学上,1个函数的梯度(gradient)指出了它的最陡增长方向。也就是说,沿着梯度的方向走,函数增长得就最快。那么沿着梯度的负方向走,函数值就下降得最快。
模型的训练目标是寻找合适的 与
以最小化代价函数值。我们先假设
与
都是一维实数,则代价函数
关于
与
的图如下所示:
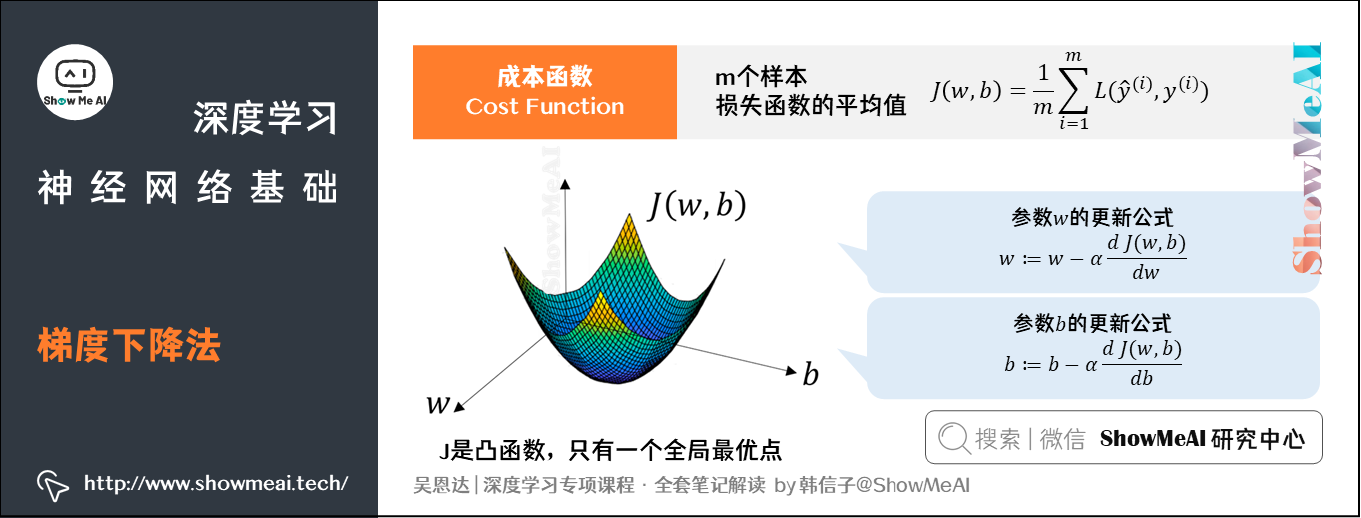
上图中的代价函数 是一个凸函数,只有一个全局最低点,它能保证无论我们初始化模型参数如何(在曲面上任何位置),都能够寻找到合适的最优解。
基于梯度下降算法,得到以下参数 的更新公式:
公式中 为学习率,即每次更新的
的步长。
成本函数 中对应的参数
更新公式为:
3.计算图(Computation Graph)

对于神经网络而言,训练过程包含了两个阶段:前向传播(Forward Propagation)和反向传播(Back Propagation)。
- 前向传播是从输入到输出,由神经网络前推计算得到预测输出的过程
- 反向传播是从输出到输入,基于Cost Function对参数
和
计算梯度的过程。
下面,我们结合一个例子用计算图(Computation graph)的形式来理解这两个阶段。
3.1 前向传播(Forward Propagation)
假如我们的Cost Function为 ,包含
、
、
三个变量。
我们添加一些中间变量,用 表示
,
表示
,则
。
整个过程可以用计算图表示:
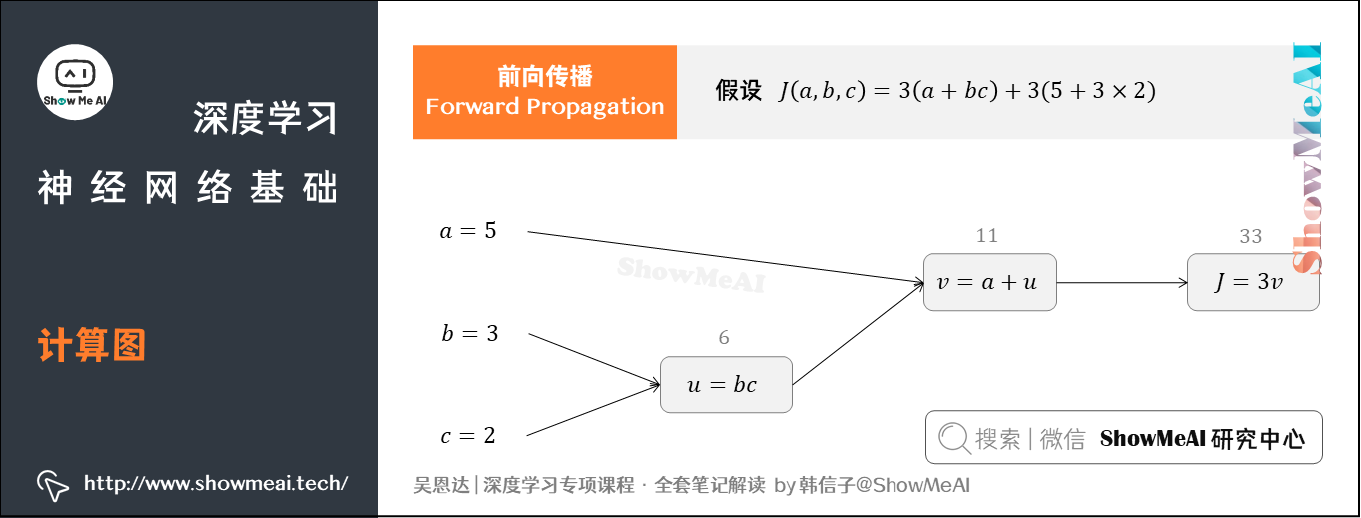
在上图中,我们让 ,
,
,则
,
,
。
计算图中,这种从左到右,从输入到输出的过程,就对应着神经网络基于 和
计算得到Cost Function的前向计算过程。
3.2 反向传播(Back Propagation)

我们接着上个例子中的计算图讲解反向传播,我们的输入参数有 、
、
三个。
① 先计算 对参数
的偏导数
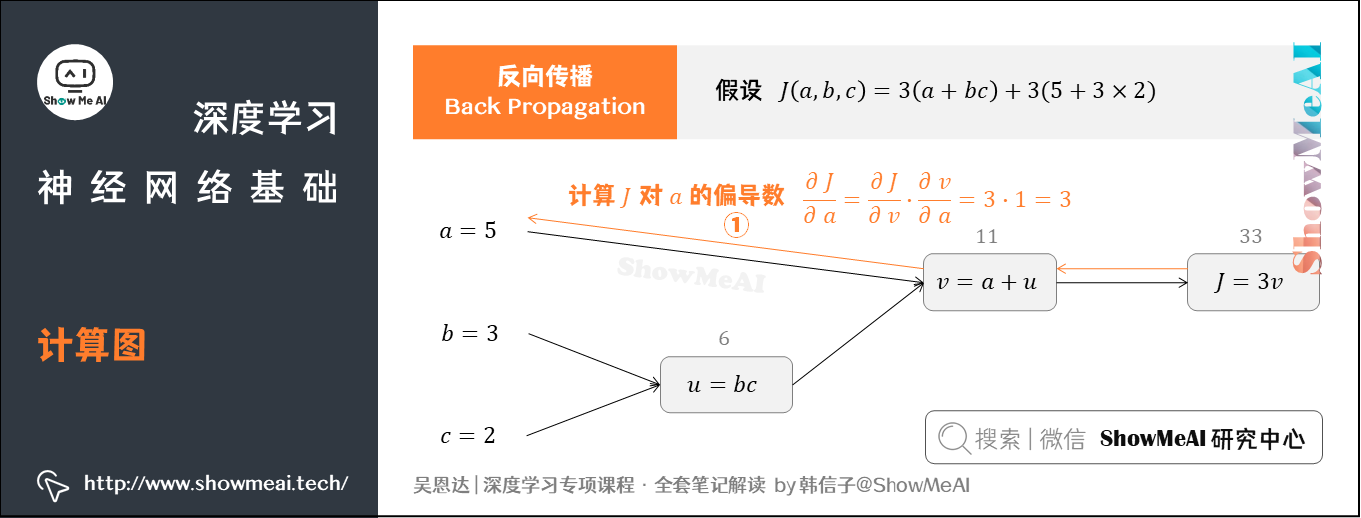
从计算图上来看,从右到左, 是
的函数,
是
的函数。基于求导链式法则得到:
② 计算 对参数
的偏导数
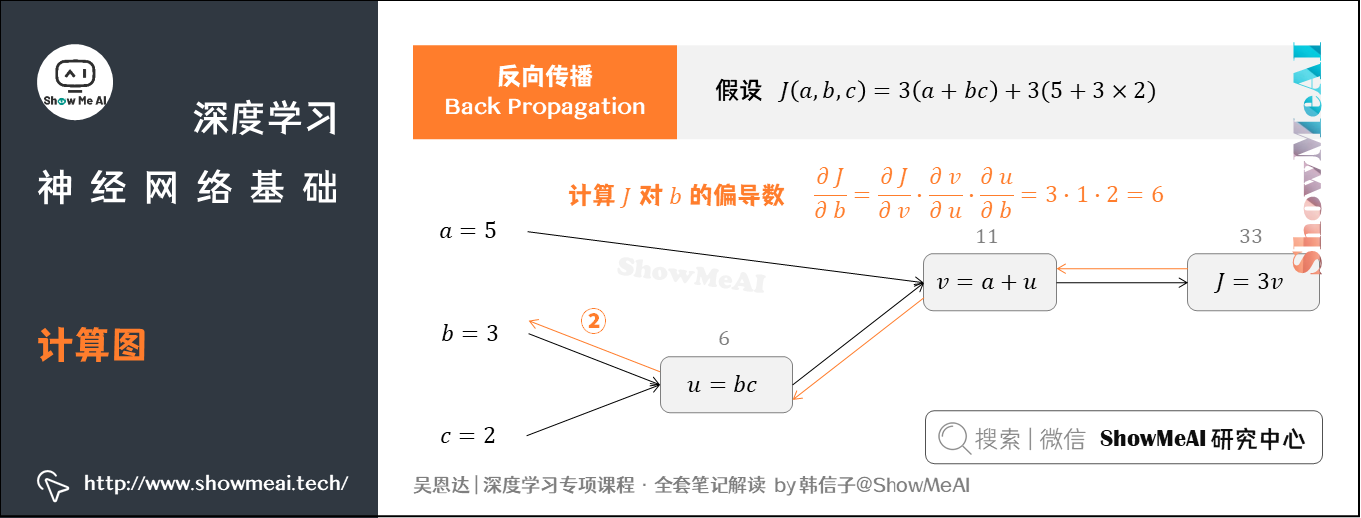
从计算图上来看,从右到左, 是
的函数,
是
的函数,
是
的函数。同样可得:
③ 计算 对参数
的偏导数
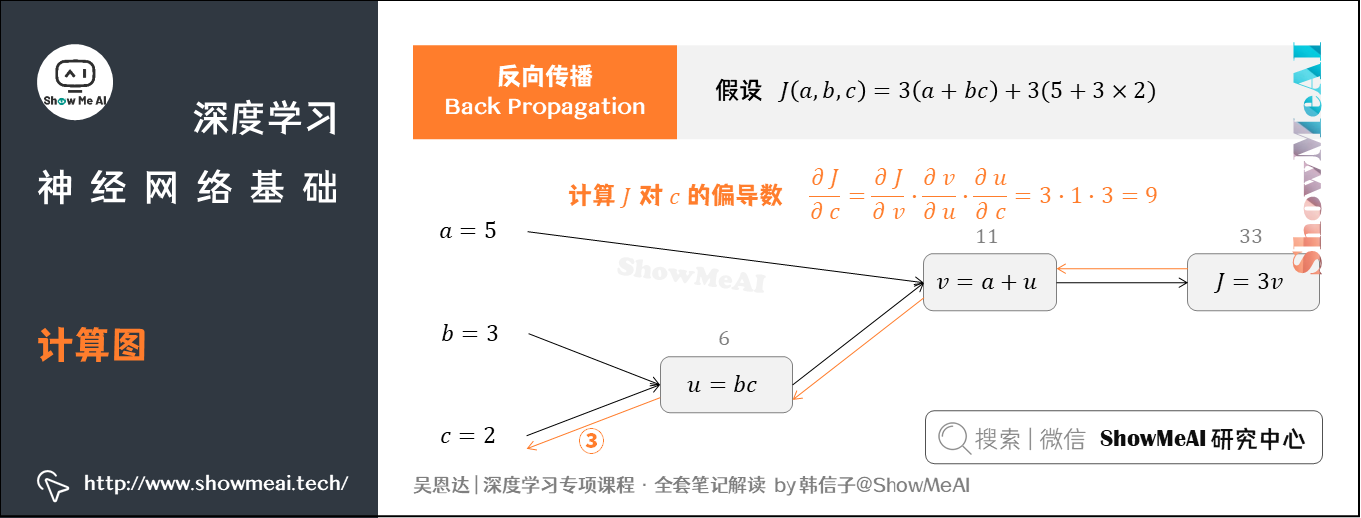
此时从右到左, 是
的函数,
是
的函数,
是
的函数。可得:
这样就完成了从右往左的反向传播与梯度(偏导)计算过程。
4.逻辑回归中的梯度下降法

回到我们前面提到的逻辑回归问题,我们假设输入的特征向量维度为2(即 ),对应权重参数
、
、
得到如下的计算图:
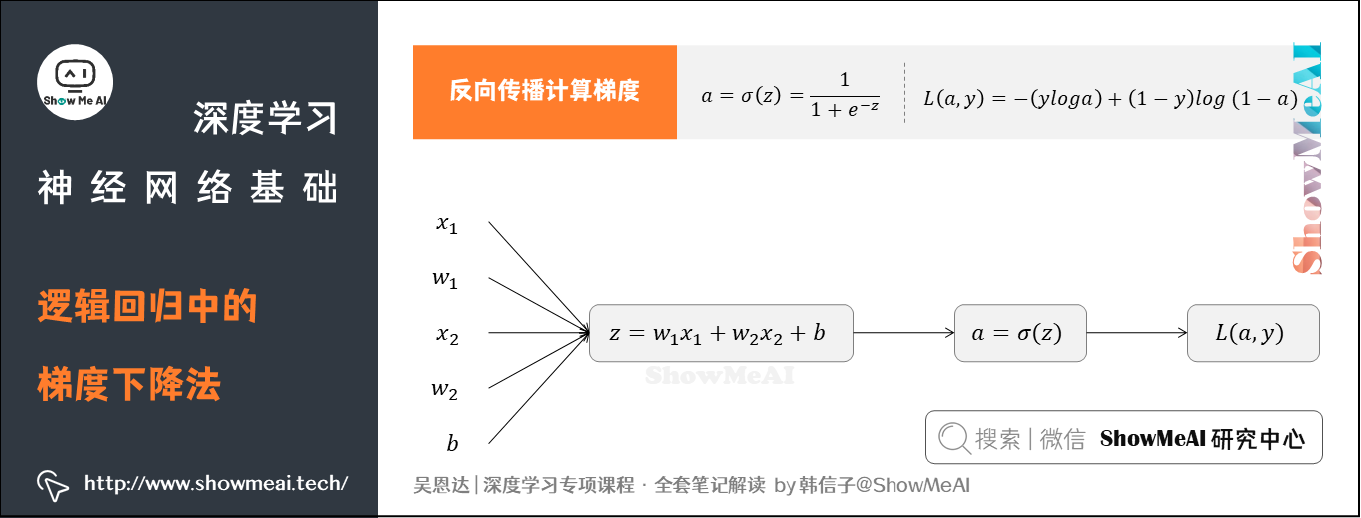
反向传播计算梯度
① 求出 对于
的导数
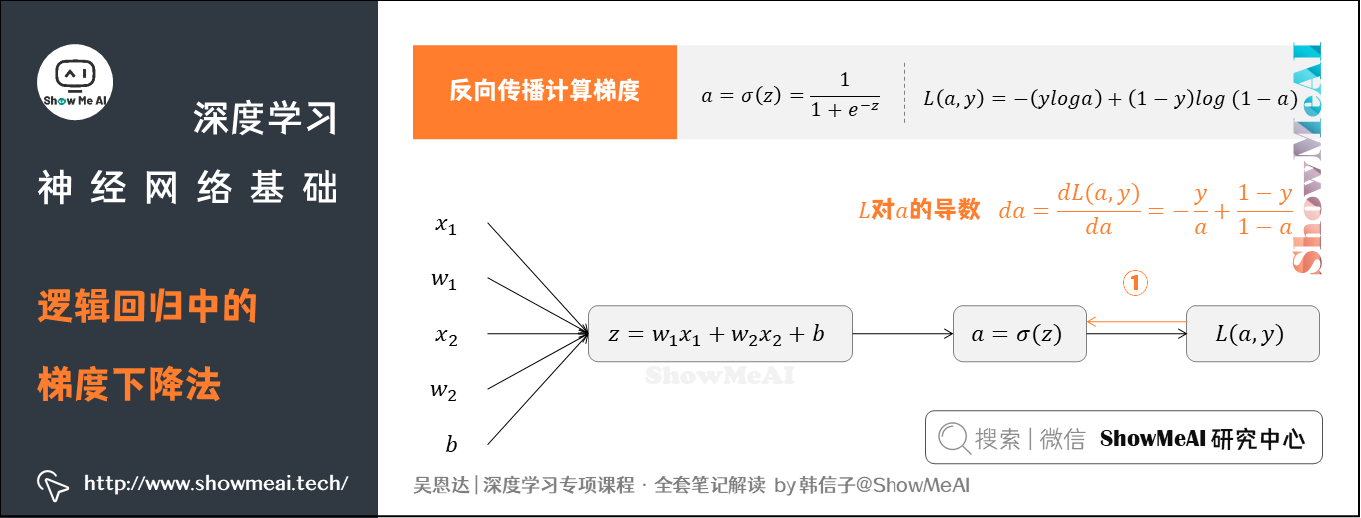
② 求出 对于
的导数
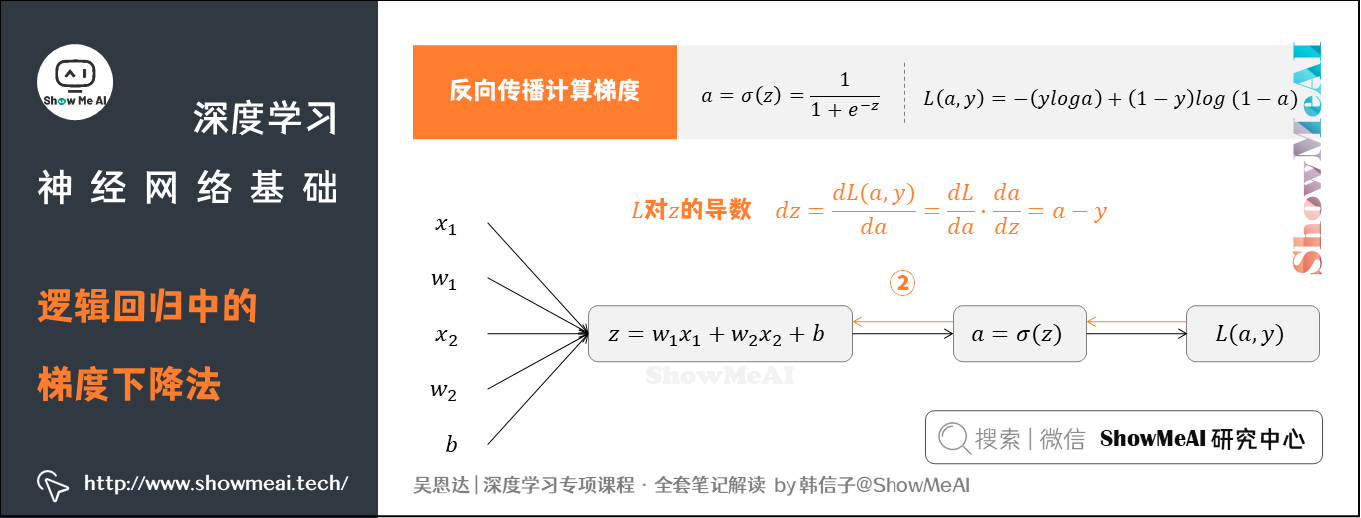
③ 继续前推计算

④ 基于梯度下降可以得到参数更新公式
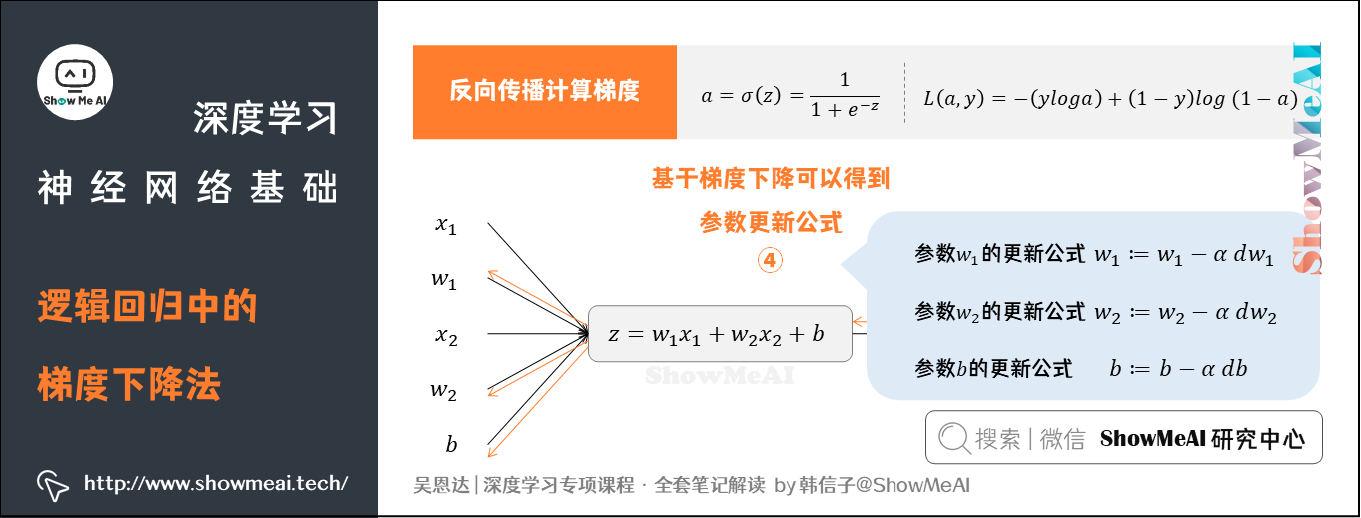


前面提到的是对单个样本求偏导和应用梯度下降算法的过程。对于有 个样本的数据集,Cost Function
、
和 权重参数
的计算如图所示。
完整的Logistic回归中某次训练的流程如下,这里仅假设特征向量的维度为2:
1 | J=0; dw1=0; dw2=0; db=0; |
接着再对 、
、
进行迭代。
上述计算过程有一个缺点:整个流程包含两个for循环。其中:
- 第一个for循环遍历
个样本
- 第二个for循环遍历所有特征
如果有大量特征,在代码中显示使用for循环会使算法很低效。向量化可以用于解决显式使用for循环的问题。
5.向量化(Vectorization)
继续以逻辑回归为例,如果以非向量化的循环方式计算 ,代码如下:
1 | z = 0;for i in range(n_x): z += w[i] * x[i]z += b |
基于向量化的操作,可以并行计算,极大提升效率,同时代码也更为简洁:
1 | z = np.dot(w, x) + b |
不用显式for循环,实现逻辑回归的梯度下降的迭代伪代码如下:
